
🧮 문제
- 크기가 N*M인 행렬 A와 M*K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N*M*K번
- 행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셉 연산 횟수의 최솟값을 구하기
🧠 접근 방법
- 결국에 최종적으로 만들어지는 두 개의 큰 행렬의 곱셈 연산 횟수를 구합니다.
참고 링크: https://youtu.be/8Ni1gaP35i8, https://youtu.be/8Ni1gaP35i8
이 문제는 행렬을 배우지 못한 세대인 제게는 볼 때부터 매우 두려운 문제였습니다. 하지만 문제에서 곱셈 연산의 수 공식을 알려주고 있기 때문에 그것만 이용하면 충분히 풀 수 있을 것 같습니다.(지금 생각해보면...) 유튜브 영상을 몇 번 돌려보고 같이 공부하는 팀원에게 설명도 몇 번 해보고, 친구의 도움도 받아서 겨우 이해한 내용을 작성합니다.


위 내용을 바탕으로 DP 테이블을 그려보면 아래와 같습니다.
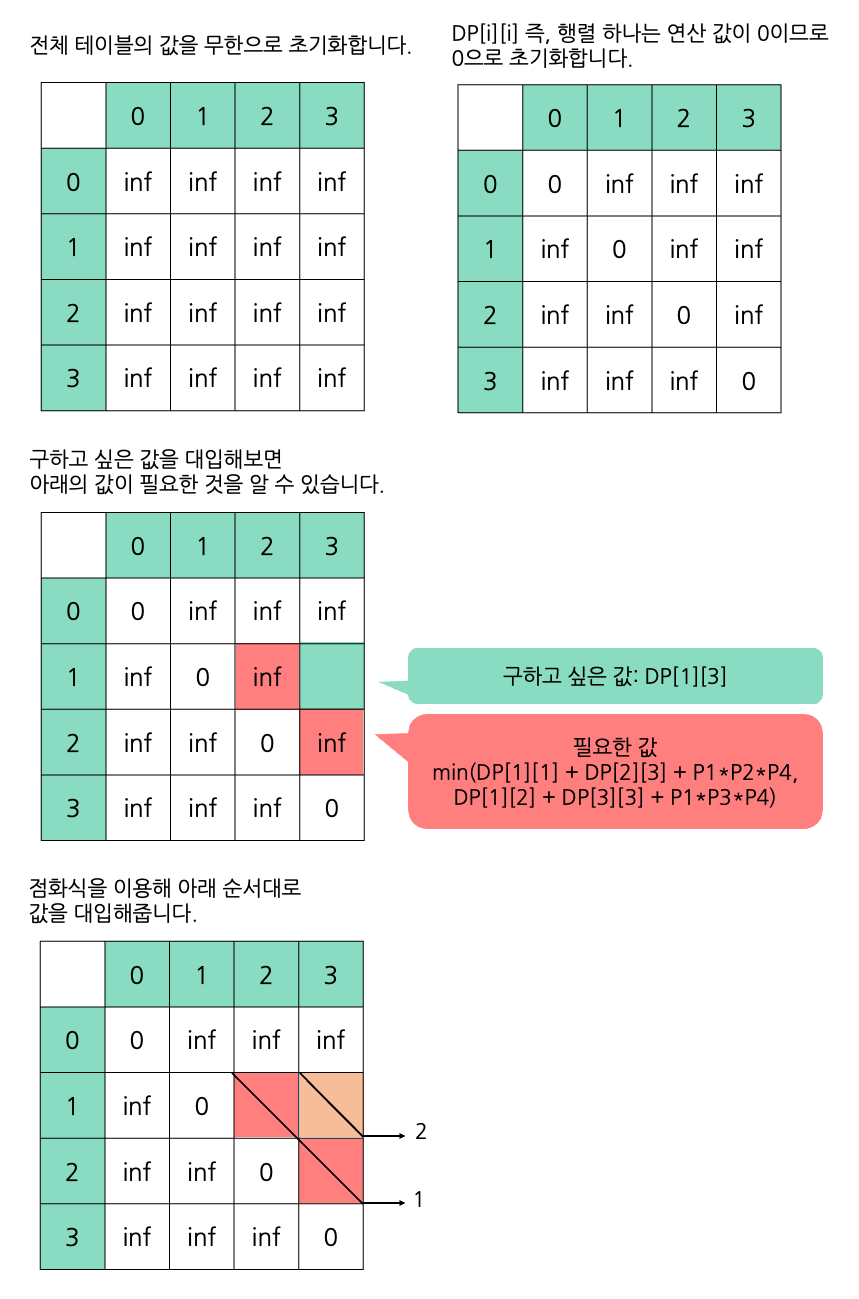
입력
- 첫째 줄: 행렬의 개수 N
- 둘째 줄~(N개): r, c(행렬의 크기)
- 항상 순서대로 곱셈을 할 수 있는 크기
출력
- 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값
👩🏻💻 코드
matrix = [[]]행렬의 정보를 담을 배열을 만들어줍니다. 이후에 인덱스를 편하게 가져오기 위해서 0번째 빈 값을 넣어줍니다.
DP = [[float("inf") for _ in range(N+1)] for _ in range(N+1)]이후에 min값을 찾을 때 방해가 되지 않도록 무한으로 초기화합니다. 0번 행, 열을 만들기 위해 행렬 개수+1 크기의 테이블을 만듭니다.
for i in range(N+1):
DP[i][i] = 0DP[i][i]값을 0으로 초기화시켜줍니다.
for a in range(N-1, 0, -1):
dif = N-a
for b in range(1, a+1):
for k in range(b, b+dif): # DP[b][] + DP[][b+dif] 이므로 b부터 b+dif-1까지 보고 싶음
DP[b][b+dif] = min(DP[b][b+dif], DP[b][k] + DP[k+1][b+dif] + matrix[b][0]*matrix[k][1]*matrix[b+dif][1])- 가장 왼쪽에 있는 대각선부터 값을 대입해줄 것이기 때문에 해당 대각선에서 값이 들어갈 칸의 개수인 N-1만큼 반복시킵니다. 그리고 칸의 i와 j 간의 차이(초깃값은 1)인 N-a를 dif 변수에 할당합니다.
오른쪽 대각선으로 갈 때마다 차이는 커지기 때문에 새롭게 반복문을 만들지 않고 줄어드는 a 변수를 사용했습니다. - 행 값이 하나씩 늘어나야 하므로 반복문을 추가했습니다.
- 마지막 for문 아래는 점화식이므로 결국에 K는 DP[b][k] + DP[k+1][b+dif]에 대입되는 수입니다. 이 수는 b부터 b+dif-1까지 가능합니다.
예를 들어 DP[1][k] + DP[k+1][3]일 때 k는 1, 2가 가능합니다. 여기서 1은 가장 처음의 b와 같고 2는 가장 마지막인 3 즉, b+dif에서 1을 뺀 것과 같습니다.
3개의 for문을 돌기 때문에 인덱스를 이해하는 것이 굉장히 중요합니다!
📑 전체 코드
# 행렬 곱셈 순서 - DP
import sys
N = int(sys.stdin.readline())
matrix = [[]]
for _ in range(N):
matrix.append(list(map(int, sys.stdin.readline().split())))
DP = [[float("inf") for _ in range(N+1)] for _ in range(N+1)]
for i in range(N+1):
DP[i][i] = 0
for a in range(N-1, 0, -1): ## 대각선에서 값이 들어갈 칸의 개수
dif = N-a # 각 칸의 i, j의 차이
for b in range(1, a+1): # i의 값
for k in range(b, b+dif): # DP[b][] + DP[][b+dif] 이므로 b부터 b+dif-1까지 보고 싶음
DP[b][b+dif] = min(DP[b][b+dif], DP[b][k] + DP[k+1][b+dif] + matrix[b][0]*matrix[k][1]*matrix[b+dif][1])
print(DP[1][N])'알고리즘 > Python' 카테고리의 다른 글
| [백준/파이썬Python] #2098 외판원 순회 : DFS를 이해합시다. 재귀도 🗺️ (0) | 2024.07.15 |
|---|---|
| [백준/파이썬Python] #2253 점프 : 퐁당퐁당 인덱스 머리쓰기 🪨 (0) | 2024.07.15 |
| [백준/파이썬Python] #9251 LCS : 문제를 부문제로 잘라보기 🛹 (0) | 2024.07.15 |
| [백준/파이썬Python] #2665 미로만들기 : 탐색할 때 중요도를 넣고 싶다면 가중치를 사용하여 힙 📓 (1) | 2024.07.15 |
| [백준/파이썬Python] #11724 연결 요소의 개수 : 끝까지 탐색해보기😵💫 (0) | 2024.07.15 |

