
🛹 문제
https://www.acmicpc.net/problem/9251
LCS(Longest Common Subsequence, 최장 공통 부분 수열), 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾기
ACAYKP 와 CAPCAK => ACAK(4개)
🧠 접근 방법
- 문자열의 가장 마지막을 비교해서 같은 경우/다른 경우를 나누는 부문제로 분할(DP, 다이나믹 프로그래밍)
참고 영상: https://youtu.be/EAXDUxVYquY
여러 블로그를 참고했지만 다들 DP 테이블에 값을 넣는 법을 주로 적어두어서 대체 DP 테이블의 규칙이 왜 그렇게 되는지 이해가 안돼서 받아들이지를 못했다. 그래서 강의를 찾아보았고 결국에는 최종 문자열을 작은 문자열로 쪼개서 생각한다는 DP적 사고 방식을 통해 나온 점화식으로 만들어진 규칙이라는 것을 알게 되었다.
💡 DP
1. 해를 분석, 부문제로 분할하기
2. 부문제의 해로 큰 문제의 해를 표현하기(점화식)
3. 적당한 순서로 table을 채우는 단계
4. table에서 해를 계산. 알고리즘의 connectness 증명

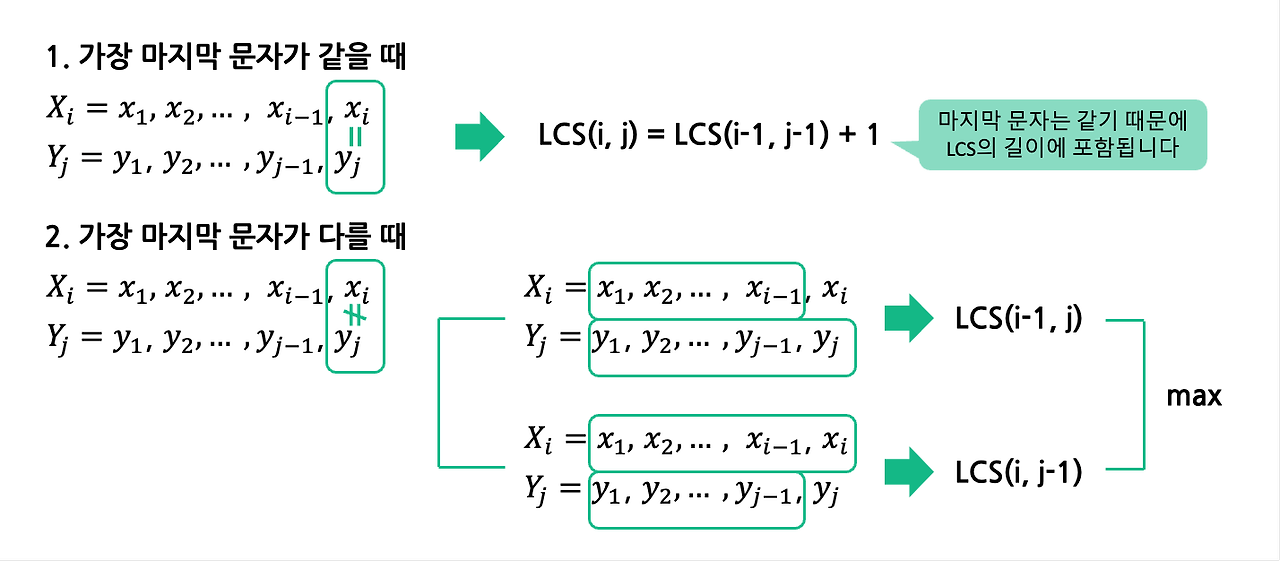
LCS는 크게 두 가지 경우로 나눌 수 있는데
1) 가장 마지막 문자가 같을 때, 2) 가장 마지막 문자가 다를 때
입니다.
1번의 경우는 가장 마지막 문자을 제외한 그 앞까지의 문자열끼리의 LCS를 구하고 마지막 문자를 더하면 됩니다.
2번의 경우에는 다시 2가지 경우로 나뉘게 되는데,
2-1) 첫번째 문자열의 가장 마지막 문자를 제외한 문자열과 두번째 문자열의 LCS
2-2) 첫번째 문자열과 두번째 문자열의 가장 마지막 문자를 제외한 문자열의 LCS
이 둘 중에서 큰 것이 LCS가 됩니다.
세운 점화식을 바탕으로 DP테이블을 만들면 아래와 같습니다.

입력
- 첫째 줄, 둘째 줄: 두 문자열
출력
- 두 문자열의 LCS의 길이
👩🏻💻 코드
📑 전체 코드
# LCS - DP
import sys
A = [0] + list(sys.stdin.readline().strip())
B = [0] + list(sys.stdin.readline().strip())
DP = [[0 for _ in range(len(A))] for _ in range(len(B))]
for i in range(1, len(B)):
row = DP[i]
before = DP[i-1]
for j in range(1, len(A)):
if B[i] == A[j]: ## 가장 마지막이 같을 때
row[j] = before[j-1] + 1
else: ## 가장 마지막이 다를 때
row[j] = max(before[j], row[j-1])
print(DP[-1][-1])'알고리즘 > Python' 카테고리의 다른 글
| [백준/파이썬Python] #2098 외판원 순회 : DFS를 이해합시다. 재귀도 🗺️ (0) | 2024.07.15 |
|---|---|
| [백준/파이썬Python] #2253 점프 : 퐁당퐁당 인덱스 머리쓰기 🪨 (0) | 2024.07.15 |
| [백준/파이썬Python] #11049 행렬곱셈순서 : 인덱스를 주의합시다... 🧮 (0) | 2024.07.15 |
| [백준/파이썬Python] #2665 미로만들기 : 탐색할 때 중요도를 넣고 싶다면 가중치를 사용하여 힙 📓 (1) | 2024.07.15 |
| [백준/파이썬Python] #11724 연결 요소의 개수 : 끝까지 탐색해보기😵💫 (0) | 2024.07.15 |

