
😵💫 문제
https://www.acmicpc.net/problem/11724
- 무방향 그래프
- 연결 요소의 개수를 구하라
그래프의 연결 요소(connected component)란?
그래프 내에서 서로 연결된 정점들의 최대 부분집합을 의미합니다. 즉, 그래프 내에서 임의의 두 정점을 선택했을 때 그 두 정점을 서로 연결하는 경로가 존재하면 이 두 정점은 같은 연결 요소에 속하게 됩니다. 하지만 서로 연결되어 있지 않은 정점들의 집합은 각각 다른 연결 요소를 형성합니다.
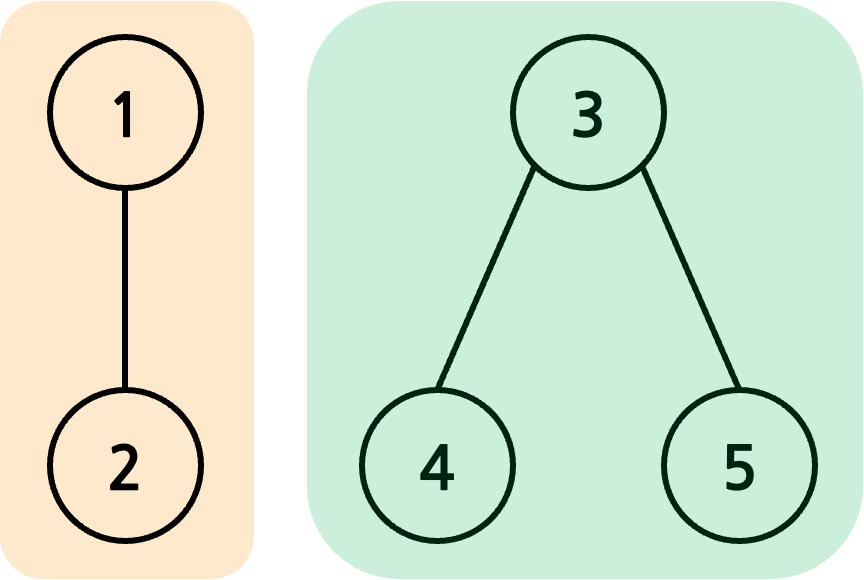
예를 들어 1과 2는 같은 연결 요소에 속하게 되고 1과 3은 다른 연결 요소에 속하게 됩니다. 위의 그래프에서는 주황색과 초록색, 두 개의 연결 요소가 존재합니다.
🧠 접근 방법
- 정점을 선택해서 해당 정점에서 이어지는 모든 정점을 탐색한다.(DFS 사용)
- 탐색 완료한 횟수를 센다.
사실 그래프의 연결 요소가 무엇인지, 탐색 방법에 무엇이 있는지만 안다면 접근은 어렵지 않은 문제다. 물론 나는 그래프의 연결 요소가 뭔지 몰라서 검색해 보았다.
입력
- 첫째 줄: N(정점의 개수), M(간선의 개수)
- 둘째 줄~: u, v(간선의 양 끝점)
출력
- 연결 요소의 개수
👩🏻💻 코드
일단 입력을 받고 연결 리스트를 만들어줍니다. 방향이 없기 때문에 간선을 잇는 양쪽 노드 모두에 추가해줍니다.
graph = [[] for _ in range(N+1)]
for i in input:
graph[i[0]].append(i[1])
graph[i[1]].append(i[0])연결 리스트에 정점이 없으면 방문 기록을 업데이트해서 나중에 방문하지 않도록 하고, 정점이 있으면 DFS 함수를 실행합니다. 결국에, DFS에서 하나의 연결 요소 안에 있는 모든 노드를 탐색하기 때문에 DFS가 실행되는 횟수가 연결 요소의 개수가 됩니다.
for i in range(1, len(visited)):
if not visited[i]:
## 🚨 정점이 없는 경우는 굳이 DFS를 하면서 시간을 낭비할 필요가 없음
if not graph[i]:
el += 1
visited[i] = 1
else:
DFS(i)
## 탐색이 끝날 때마다 실행하고 싶을 때 재귀함수 안에 넣으면 복잡함
## 🚨 재귀함수 바깥에서 세기
el += 1여기서 블로그 코드를 참고했는데 참고했던 이유는 연결 요소의 개수를 셀 때 DFS 함수 안에서 종료 조건을 걸고 종료 조건이 되면 연결 요소의 개수를 늘리려고 했는데 DFS가 재귀함수이다 보니 계속 반복해서 원하는 결과가 나오지 않았습니다.
💡 탐색이 끝날 때마다 실행하고 싶을 때는 재귀함수 안에 넣지말고 재귀함수 바깥에서 세기!
📑 전체 코드
# 연결 요소의 개수
import sys
sys.setrecursionlimit(10**6)
N, M = map(int, sys.stdin.readline().split())
input = []
for _ in range(M):
input.append(list(map(int, sys.stdin.readline().split())))
## 연결 리스트 만들기
graph = [[] for _ in range(N+1)]
for i in input:
graph[i[0]].append(i[1])
graph[i[1]].append(i[0])
for i in input:
i = sorted(i)
## DFS
el = 0
visited = [0]*(N+1)
def DFS(start):
global el, visited
visited[start] += 1
for i in graph[start]:
if visited[i] == 0:
DFS(i)
## 블로그 코드 참고 =====================================
for i in range(1, len(visited)):
if not visited[i]:
## 🚨 정점이 없는 경우는 굳이 DFS를 하면서 시간을 낭비할 필요가 없음
if not graph[i]:
el += 1
visited[i] = 1
else:
DFS(i)
## 탐색이 끝날 때마다 실행하고 싶을 때 재귀함수 안에 넣으면 복잡함
## 🚨 재귀함수 바깥에서 세기
el += 1
print(el)'알고리즘 > Python' 카테고리의 다른 글
| [백준/파이썬Python] #2098 외판원 순회 : DFS를 이해합시다. 재귀도 🗺️ (0) | 2024.07.15 |
|---|---|
| [백준/파이썬Python] #2253 점프 : 퐁당퐁당 인덱스 머리쓰기 🪨 (0) | 2024.07.15 |
| [백준/파이썬Python] #11049 행렬곱셈순서 : 인덱스를 주의합시다... 🧮 (0) | 2024.07.15 |
| [백준/파이썬Python] #9251 LCS : 문제를 부문제로 잘라보기 🛹 (0) | 2024.07.15 |
| [백준/파이썬Python] #2665 미로만들기 : 탐색할 때 중요도를 넣고 싶다면 가중치를 사용하여 힙 📓 (1) | 2024.07.15 |

