레드 블랙트리(The red black tree): 규칙, 회전, 삽입

 

• 루트 노드에서 leaf 노드로 가는 경로를 보았을 때 red black 트리는 한 경로가 다른 경로보다 2배 이상 길지 않다. 그래서 대체적으로 균형잡혀 있다.
• 각각의 노드는 color, key, left, right, p 속성을 가지고 있다.
• red black 트리는 아래 규칙을 만족하는 이진 탐색 트리이다.

규칙

• 모든 노드는 색을 가진다. (red 또는 black)
• 루트 노드는 black
• 모든 leaf 노드는 NIL, black
• red 노드는 red 자식 노드를 가질 수 없다.(2개의 black 자식을 가져야 한다.)
• 각 노드에서 leaf 노드로 가는 경로들은 같은 수의 black 노드를 가지고 있어야 한다.

회전

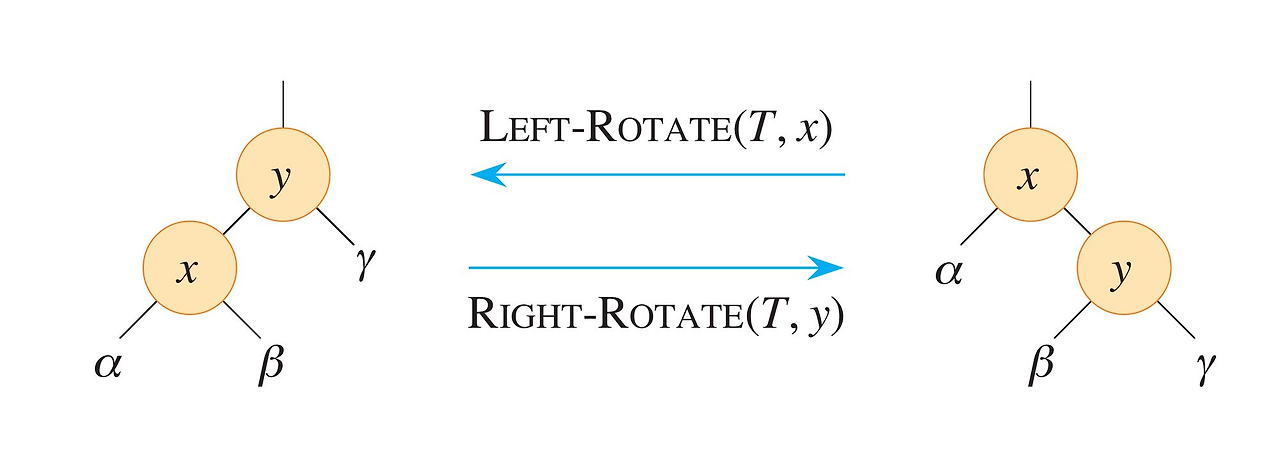
Left-Rotate 왼쪽 회전

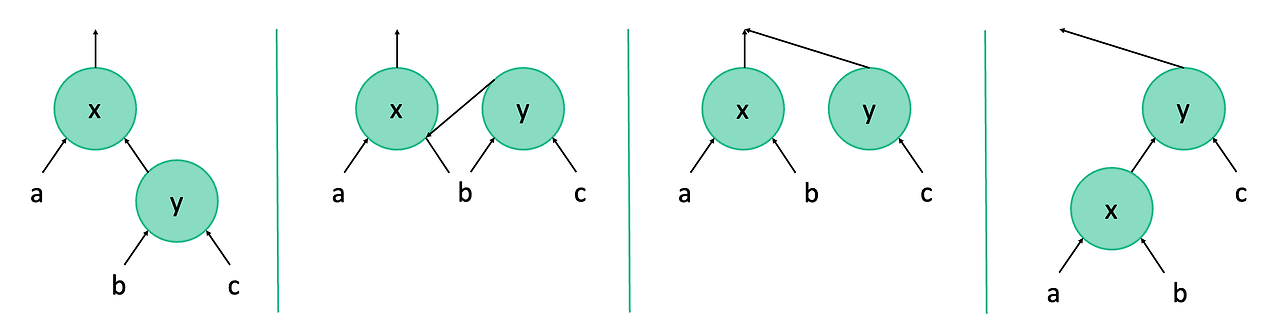
1. y의 왼쪽 서브트리는 x의 오른쪽 서브 트리가 된다.(바꾼다라는 표현이 헷갈림)
2. y의 왼쪽 서브트리가 T.nil이 아니라면(비어있지 않다면)
   y의 왼쪽 서브트리는 x를 가리키게 된다.(x의 자식 노드가 된다.)
3. y가 가리키는 곳이(포인터가) x가 가리키는 곳이 된다. 즉 y는 이제 x의 부모를 가리킨다.
4. 만약 x의 포인터가 T.nil을 가리킨다면, 즉 루트 노드였다면 이제는 y가 루트 노드가 된다.
   만약 x가 왼쪽 자식 노드였다면, y는 x의 부모의 왼쪽 자식 노드가 된다.
   만약 x가 오른쪽 자식 노드였다면, y는 x 부모의 오른쪽 자식 노드가 된다.
5. 그러고 x를 y의 왼쪽 자식 노드로 만든다.
6. x의 부모를 y로 만든다.

삽입(T에 z 넣기)

x = T.root
y = T.nil
while x =/= T.nil
	y = x
	if z.key < x.key
		x = x.left
	else x = x.right
z.p = y
if y == T.nil
	T.root = z
elseif z.key < y.key
	y.left = z
else y.right = z
z.left = T.nil
z.right = T.nil
z.color = RED
RB-INSERT-FIXUP(T, z)

1. x = T.root
   삽입하고자 하는 z와 비교될 대상 노드입니다.
2. y = T.nil
   삽입하고자 하는 z의 부모 노드가 될 노드입니다. 현재는 x의 부모 노드입니다.
3. <삽입할 새로운 노드의 위치를 찾기 위한 과정>
   현재 노드 x가 트리의 끝(T.nil)에 도달할 때까지 반복합니다.
   y 변수에 x 값을 대입합니다. y는 계속해서 x의 부모가 됩니다.
   탐색하면서 z의 키 값이 x의 키 값보다 작으면 x의 왼쪽 서브트리를 탐색하고, 크면 오른쪽 서브트리를 탐색합니다.
4. z가 들어갈 곳을 찾았으면, z가 y를 가리키게 합니다.(z의 부모 포인터를 y로 설정합니다.)
5. 만약 y가 T.nil이면 z가 새로운 루트 노드입니다.
   z가 루트 노드가 아니고 z의 키 값이 y의 키 값보다 작으면 z는 y의 왼쪽 자식 노드가 됩니다.
   z가 루트 노드가 아니고 z의 키 값이 y의 키 값보다 크면 z는 y의 오른쪽 자식 노드가 됩니다.
6. z의 자식 노드를 T.nil로 설정하고 새로운 노드 z를 red로 설정합니다.
7. 그리고 RB-INSERT-FIXUP 함수를 통해 새로운 노드가 추가된 red-black tree를 정리해줍니다.

RB-INSERT-FIXUP(T, z)
while z.p.color == RED
	if z.p == z.p.p.left
		y = z.p.p.right
		if y.color == RED
			z.p.color = BLACK
			y.color = BLACK
			z.p.p.color = RED
			z = z.pp
		else
			if z == z.p.right
				z = z.p
				LEFT-ROTATE(T, z)
			z.p.color = BLACK
			z.p.p.color = RED
			RIGHT-ROTATE(T, z.p.p)
	else
		y = z.p.p.left
		if y.color == RED
			z.p.color = BLACK
			y.color = BLACK
			z.p.p.color = RED
			z = z.p.p
		else
			if z == z.p.left
				z = z.p
				RIGHT-ROTATE(T, z)
			z.p.color = BLACK
			z.p.p.color = RED
			LEFT-ROTATE(T, z.p.p)
T.root.color = Black
		

RB 트리에 노드를 삽입한 후, RB 트리의 조건을 만족하도록 하는 함수

1. while 루프를 사용하여 새로 삽입된 노드의 부모 노드가 빨간색동안 반복합니다.
2. 만약 z의 부모가 왼쪽 자식이라면
   1. y는 z의 오른쪽 삼촌
   2. 만약 y의 색이 빨강이라면
      1. z의 부모(y의 형제) 노드는 검정색
      2. y의 색은 검정색
      3. z의 조부모 노드의 색은 빨간색
      4. z를 z의 조부모 노드로 이동합니다.
   3. 만약 y의 색이 검정이라면
      1. z가 z 부모 노드의 오른쪽 자식이라면
         1. z는 z의 부모 노드로 이동합니다.
         2. 그리고 왼쪽으로 회전합니다.
      2. z의 부모 노드는 검정색
      3. z의 조부모 노드는 빨간색
      4. 오른쪽으로 회전합니다.
3. 만약 z의 부모가 오른쪽 자식이라면
   1. y는 z의 왼쪽 삼촌
   2. 만약 y의 색이 빨강이라면
      1. z의 부모 노드는 검정색
      2. y의 색은 검정색
      3. z의 조부모 색은 빨간색
      4. z는 z의 조부모 노드로 이동합니다.
   3. 만약 y의 색이 검정이라면
      1. z가 z 부모 노드의 왼쪽 자식이라면
         1. z는 z의 부모 노드로 이동합니다.
         2. 그리고 오른쪽으로 회전합니다.
      2. z의 부모의 색은 검정색
      3. z의 조부모의 색은 빨간색
      4. 왼쪽으로 회전합니다.
4. 루트의 색상을 검정색으로 바꿉니다.

참고 자료

• Introduction to Algorithms - Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein

* C언어로 작성한 코드는 https://github.com/SeryeongK/rbtree-lab 에 있습니다.